A real-world case (Biomimetics: space technology)

Here we use a some data produced by precisely modelling a nanostructured solar array inspired by the moth eye. We analyze the relations (found by dcgpy symbolic_regression using mes) between the cell efficiency and 12 different model parameters (thickness, etc..).

The data were generated in the context of the European Space Agency Ariadna study on bio-inspired solar cells (http://www.esa.int/gsp/ACT/projects/diatom/).
The fits were generated evolving 126 populations (size 8) via dcgpy.mes(10000, max_mut=15) on an AMD EPYC 7702 64-Core Processor (~20 minutes to complete)

Data points are pickled into a file named moth_data.pk in the form of a tuple of two arrays Xs, Ys.

The fitted expressions are pickled into a file named result.pk in a list: result[prob_id][0] = fitnesses result[prob_id][1] = chromosomes

This tutorial is informative as it shows the wide diversity and quality of models produced by unconnected evolutions and their difference with respect to the fit error.

Preliminaries

[1]:

# Core imports
import dcgpy # This was compiled in bertha from github HEAD (v1.5 is unreleased)
import pygmo as pg
import numpy as np
# Sympy is nice to have for basic symbolic manipulation.
from sympy import init_printing
from sympy.parsing.sympy_parser import *
init_printing()
# Plotting
%matplotlib inline
import matplotlib.pyplot as plt
# Pickling
import pickle as pk

[2]:

# Load the data to fit
with open("moth_data.pk", "rb") as f:
    Xs,Ys  = pk.load(f)
# Load the best solutions found running dcgpy.mes(10000, max_mut=15) on 126 separate runs
#with open("eph_3_r_1_c_16_lb_17_sum_diff_mul_diff_exp.pk", "rb") as f:
with open("eph_4_r_1_c_16_lb_15_sum_diff_mul_div_exp_gaussian.pk", "rb") as f:
    results = pk.load(f)
kernel_list = ["sum", "diff", "mul", "div", "exp", "gaussian"]

[3]:

# We define the kernel set that was used to produce the runs
ss = dcgpy.kernel_set_double(kernel_list)

[4]:

# Since we have not pickled all the objects used during the experiment, we need to reconstruct the
# udp and the data in a good format.
def reconstruct_udp(prob_id):
    X = np.reshape(Xs[prob_id], (len(Xs[prob_id]),1))
    Y = np.reshape(Ys[prob_id], (len(Ys[prob_id]),1))
    udp = dcgpy.symbolic_regression(points = X, labels = Y, kernels=ss(), n_eph=4, rows =1, cols=16, levels_back=17, multi_objective=False)
    return (udp, X, Y)

[5]:

# We also want to know (at a glance) if the experimental setup worked well in terms of MSEs
mses = [min(a[0]) for a in results]
print("Best  fit: prob-id ", np.argmin(mses), "| Value: ", mses[np.argmin(mses)][0])
print("Worst fit: prob-id ", np.argmax(mses), "| Value: ", mses[np.argmax(mses)][0])
print("On average: ", sum(mses)/len(mses))

Best  fit: prob-id  4 | Value:  3.359546731194255e-06
Worst fit: prob-id  0 | Value:  2.3801558148325692e-05
On average:  [1.0948612e-05]

The best fits found

[6]:

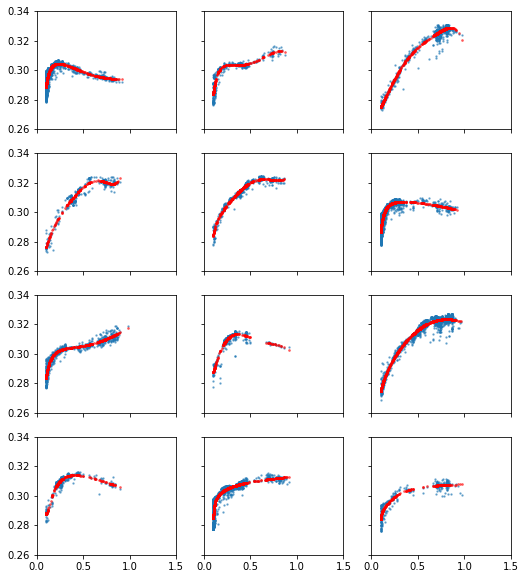
# The data and best fits at a glance
fig, axes = plt.subplots(nrows = 4, ncols=3, sharex=True, sharey=True, figsize=(8.5,10))
for i, ax in enumerate(np.reshape(axes,(12))[:12]):
    udp, X, Y = reconstruct_udp(i)
    ax.scatter(X, Y, s=2.0, alpha=0.5)
    best_run = np.argmin(results[i][0])
    best_dv = results[i][1][best_run]
    Y_pred = udp.predict(X, best_dv)
    ax.scatter(X, Y_pred, s=3.0, alpha=0.5, c = 'r')

ax.set_xlim(0, 1.5)
ax.set_ylim(0.26, 0.34)

[6]:

$\displaystyle \left( 0.26, \ 0.34\right)$

../_images/notebooks_real_world3_8_1.png

[7]:

# Lets peek into the best fits functional forms. Each of the 12 problems is here
## assigned an id
from IPython.display import display, Math
for prob_id in range(12):
    udp, X, Y = reconstruct_udp(prob_id)
    best_run= np.argmin(results[prob_id][0])
    best_x = results[prob_id][1][best_run]
    best_f = results[prob_id][0][best_run]
    s = parse_expr(udp.prettier(best_x))[0].simplify()
    display("prob_id: {}, err: {}".format(prob_id, best_f[0]), Math(r'{}'.format(s._repr_latex_())))

# NOTE: selecting the fit with the best MSE may not be ideal as best formulas do get unnecessarily complex

'prob_id: 0, err: 2.3801558148325692e-05'

$\displaystyle \displaystyle - c_{1} - \frac{c_{2}}{x_{0}} + \frac{c_{2}}{2 x_{0}^{2}} + c_{3} e^{- 4 x_{0}^{2}} - c_{4} x_{0} e^{- 4 x_{0}^{2}} + c_{4}$

'prob_id: 1, err: 1.5481952594443556e-05'

$\displaystyle \displaystyle \frac{c_{1} - c_{2} e^{x_{0}} + x_{0} \left(c_{2} e^{x_{0}} + c_{2} - c_{4} - x_{0} + \left(- c_{1} + c_{2} e^{x_{0}} + c_{3}\right) e^{x_{0}}\right)}{x_{0}}$

'prob_id: 2, err: 4.866500757662433e-06'

$\displaystyle \displaystyle \left(c_{1} + c_{4} x_{0} + \left(- c_{3} + \left(c_{2} - x_{0}\right) e^{\left(x_{0}^{2} e^{x_{0}^{2}} - 1\right) e^{- x_{0}^{2}}}\right) e^{x_{0}^{2}}\right) e^{- x_{0}^{2}}$

'prob_id: 3, err: 7.993101895616535e-06'

$\displaystyle \displaystyle - c_{1} x_{0} e^{x_{0}^{2}} + c_{1} + c_{2} e^{x_{0}^{2}} + c_{3} - c_{4} x_{0} + e^{- e^{- 2 x_{0}^{2}}} - e^{- x_{0}^{2}}$

'prob_id: 4, err: 3.359546731194255e-06'

$\displaystyle \displaystyle c_{1} x_{0} - c_{2} + c_{3} e^{- x_{0}} + c_{4} - \frac{c_{4}}{x_{0}} - e^{- e^{2 x_{0}}}$

'prob_id: 5, err: 1.686027444316002e-05'

$\displaystyle \displaystyle c_{1} x_{0} + c_{1} e^{- x_{0}^{4}} + \frac{c_{1}}{x_{0}^{2}} + c_{2} - 2 c_{3} - \frac{c_{3}}{x_{0}^{3}} - 2 c_{4} x_{0} - \frac{c_{4}}{x_{0}^{2}}$

'prob_id: 6, err: 9.922429392571683e-06'

$\displaystyle \displaystyle - c_{2} - c_{3} e^{- x_{0}^{2}} + \frac{2 c_{4}}{c_{1} + x_{0}} - e^{- \left(c_{1} + x_{0}\right)^{2}} + e^{- c_{4}^{2}}$

'prob_id: 7, err: 8.515167695863056e-06'

$\displaystyle \displaystyle - c_{1} e^{e^{- x_{0}^{2}}} + c_{2} + c_{3} x_{0} - c_{4} e^{- x_{0}^{2}} + x_{0} e^{- x_{0}^{2}}$

'prob_id: 8, err: 5.7033656245193685e-06'

$\displaystyle \displaystyle \frac{\left(x_{0} \left(c_{1} x_{0} - c_{3} + e^{c_{2}}\right) e^{c_{1} x_{0} \left(c_{3} - e^{c_{2}}\right)} + \left(- c_{2} x_{0} + c_{4}\right) e^{x_{0}^{2}}\right) e^{- x_{0} \left(c_{1} \left(c_{3} - e^{c_{2}}\right) + x_{0}\right)}}{x_{0}}$

'prob_id: 9, err: 4.523905989067585e-06'

$\displaystyle \displaystyle 2 c_{1} + \frac{c_{1}}{x_{0}^{2}} + c_{2} - c_{3} x_{0} + \frac{4 c_{4}}{x_{0}} + \frac{c_{4}}{x_{0}^{3}}$

'prob_id: 10, err: 1.9017543270061446e-05'

$\displaystyle \displaystyle \frac{c_{2} e^{\frac{1}{x_{0}}} - c_{3} + x_{0} \left(- c_{1} x_{0} + c_{4}\right)}{x_{0}}$

'prob_id: 11, err: 1.1337997121125522e-05'

$\displaystyle \displaystyle \frac{c_{2} \left(c_{4} - x_{0}^{4}\right) - c_{3} x_{0} \left(c_{4} - x_{0}^{4}\right) + x_{0} \left(- c_{1} x_{0}^{2} - c_{2} x_{0} + c_{4}\right)}{x_{0} \left(c_{4} - x_{0}^{4}\right)}$

Looking for elegant forms

Some of the best fits found seem to be unnecessarily complex, we here look in the results for more elegant forms with a marginally worse MSA

[8]:

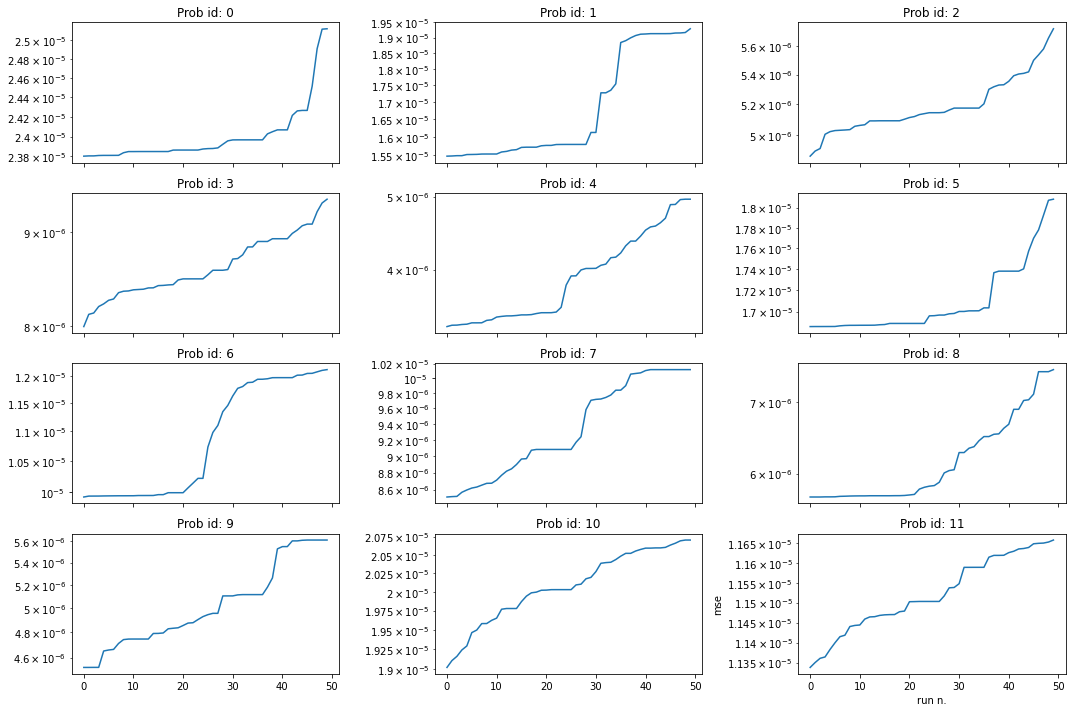
# Lets take for each problem the best 50 fits found and plot the corresponding final MSE
fig, axes = plt.subplots(nrows = 4, ncols=3, sharex=True, figsize=(15,10))
for i, ax in enumerate(np.reshape(axes,(12))[:12]):
    a = results[i]
    ax.semilogy(sorted(a[0])[:50])
    ax.title.set_text("Prob id: " + str(i))
plt.xlabel("run n.")
plt.ylabel("mse")
plt.tight_layout()
# Conclusion: there are many formulas with similar error that can be considered as equally good fits

../_images/notebooks_real_world3_11_0.png

Showing the best 5 fits

[9]:

for prob_id in range(12):
    print("---------------------------------------------------------")
    print("Best five fits for id: ", prob_id)
    a = results[prob_id]
    fits = a[0]
    best_idxs = sorted(range(126), key = lambda x: fits[x])
    for best_isl in best_idxs[:5]:
        best_x = a[1][best_isl]
        best_f = a[0][best_isl]
        udp, X, Y = reconstruct_udp(prob_id)
        s = parse_expr(udp.prettier(best_x))[0].simplify()
        display("prob_id: {}, err: {}".format(prob_id, best_f[0]), Math(r'{}'.format(s._repr_latex_())))
    print("---------------------------------------------------------")

---------------------------------------------------------
Best five fits for id:  0

'prob_id: 0, err: 2.3801558148325692e-05'

$\displaystyle \displaystyle - c_{1} - \frac{c_{2}}{x_{0}} + \frac{c_{2}}{2 x_{0}^{2}} + c_{3} e^{- 4 x_{0}^{2}} - c_{4} x_{0} e^{- 4 x_{0}^{2}} + c_{4}$

'prob_id: 0, err: 2.380412125841117e-05'

$\displaystyle \displaystyle \frac{c_{2}}{x_{0}} + c_{3} + c_{4} \left(\frac{c_{2}}{x_{0}} - x_{0}\right)^{2} - x_{0} \left(c_{1} - \frac{x_{0}}{\frac{c_{2}}{x_{0}} - x_{0}}\right) + \frac{x_{0}}{\frac{c_{2}}{x_{0}} - x_{0}}$

'prob_id: 0, err: 2.3804219347209996e-05'

$\displaystyle \displaystyle \frac{c_{4} + \left(c_{4} + x_{0}^{2}\right) \left(- c_{1} + c_{2} x_{0} + c_{3} x_{0}^{2}\right)}{c_{4} + x_{0}^{2}}$

'prob_id: 0, err: 2.3808190703491017e-05'

$\displaystyle \displaystyle \frac{c_{1} e^{- x_{0}^{2}}}{x_{0}} - \frac{c_{2}}{x_{0}} - c_{3} - \frac{c_{4}}{x_{0}^{2}} - 1$

'prob_id: 0, err: 2.3809219218852146e-05'

$\displaystyle \displaystyle c_{1} x_{0} - c_{2} x_{0}^{2} + \frac{c_{3}}{x_{0}^{2}} - c_{4}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  1

'prob_id: 1, err: 1.5481952594443556e-05'

$\displaystyle \displaystyle \frac{c_{1} - c_{2} e^{x_{0}} + x_{0} \left(c_{2} e^{x_{0}} + c_{2} - c_{4} - x_{0} + \left(- c_{1} + c_{2} e^{x_{0}} + c_{3}\right) e^{x_{0}}\right)}{x_{0}}$

'prob_id: 1, err: 1.5486489454637892e-05'

$\displaystyle \displaystyle \frac{c_{2} x_{0} \left(1 - x_{0}\right) + \left(c_{1} + x_{0} \left(- c_{2} x_{0} + c_{2} + c_{3} x_{0} + c_{4}\right)\right) e^{x_{0}^{2}}}{x_{0}}$

'prob_id: 1, err: 1.5494780218604477e-05'

$\displaystyle \displaystyle c_{1} x_{0} + c_{2} - \frac{c_{2}}{x_{0}} - c_{3} + c_{4} e^{- e^{- 2 x_{0}^{2}}}$

'prob_id: 1, err: 1.549478021860451e-05'

$\displaystyle \displaystyle - \frac{c_{1}}{x_{0}} + c_{2} + c_{3} e^{- e^{- 2 x_{0}^{2}}} - c_{4} x_{0}$

'prob_id: 1, err: 1.5524996126148153e-05'

$\displaystyle \displaystyle - c_{1} + \frac{c_{2} e^{x_{0}^{2}}}{x_{0}} + c_{3} x_{0} + c_{4} e^{- x_{0}^{2}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  2

'prob_id: 2, err: 4.866500757662433e-06'

$\displaystyle \displaystyle \left(c_{1} + c_{4} x_{0} + \left(- c_{3} + \left(c_{2} - x_{0}\right) e^{\left(x_{0}^{2} e^{x_{0}^{2}} - 1\right) e^{- x_{0}^{2}}}\right) e^{x_{0}^{2}}\right) e^{- x_{0}^{2}}$

'prob_id: 2, err: 4.8981961254319396e-06'

$\displaystyle \displaystyle c_{1} + c_{2} x_{0}^{3} + c_{3} e^{- x_{0}^{2}} - c_{4} x_{0}^{2}$

'prob_id: 2, err: 4.9140689166325595e-06'

$\displaystyle \displaystyle c_{1} x_{0} + c_{2} e^{2 x_{0}} + 2 c_{3} e^{- x_{0}} - c_{4} + 2 e^{- x_{0}^{2}}$

'prob_id: 2, err: 5.004121929538379e-06'

$\displaystyle \displaystyle \left(\left(- c_{1} x_{0} + c_{2} x_{0} - c_{4} - x_{0}\right) e^{x_{0}^{2}} + \left(c_{2} x_{0} + c_{3} - c_{4} - x_{0}\right) e^{2 x_{0}^{2}} + 1\right) e^{- 2 x_{0}^{2}}$

'prob_id: 2, err: 5.0208570048206605e-06'

$\displaystyle \displaystyle \frac{c_{1}^{2} e^{- x_{0}}}{c_{3}} - c_{2} + c_{4} e^{- x_{0}^{2}} - e^{- \frac{c_{1}^{2}}{x_{0}^{2}}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  3

'prob_id: 3, err: 7.993101895616535e-06'

$\displaystyle \displaystyle - c_{1} x_{0} e^{x_{0}^{2}} + c_{1} + c_{2} e^{x_{0}^{2}} + c_{3} - c_{4} x_{0} + e^{- e^{- 2 x_{0}^{2}}} - e^{- x_{0}^{2}}$

'prob_id: 3, err: 8.116838729621195e-06'

$\displaystyle \displaystyle c_{1} x_{0} + c_{2} e^{e^{2 x_{0}}} + c_{3} e^{x_{0}} + c_{4} + e^{- e^{2 x_{0}}}$

'prob_id: 3, err: 8.13057337419324e-06'

$\displaystyle \displaystyle \left(c_{3} + \left(c_{3} + \left(c_{2} + e^{x_{0}}\right) e^{x_{0}}\right) \left(e^{x_{0}} + e^{e^{x_{0}}}\right) + \left(- c_{1} e^{x_{0} + e^{x_{0}}} + c_{2} - c_{4} + e^{x_{0}}\right) e^{x_{0}}\right) e^{- x_{0}}$

'prob_id: 3, err: 8.19691765672383e-06'

$\displaystyle \displaystyle c_{2} + x_{0} \left(c_{1} x_{0} - c_{3}\right) - x_{0} + \left(c_{2} - x_{0}\right) e^{x_{0}} + \left(- c_{2} - c_{4} + x_{0}\right) e^{x_{0}^{2}}$

'prob_id: 3, err: 8.224153596665173e-06'

$\displaystyle \displaystyle c_{1} + 2 c_{4} x_{0} - \left(c_{2} + c_{3} e^{x_{0}^{2}}\right) e^{x_{0}^{2}} - e^{c_{2}} + e^{x_{0}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  4

'prob_id: 4, err: 3.359546731194255e-06'

$\displaystyle \displaystyle c_{1} x_{0} - c_{2} + c_{3} e^{- x_{0}} + c_{4} - \frac{c_{4}}{x_{0}} - e^{- e^{2 x_{0}}}$

'prob_id: 4, err: 3.3734252967348888e-06'

$\displaystyle \displaystyle c_{1} - c_{2} x_{0} - \frac{c_{3}}{x_{0}} - c_{4} e^{e^{- 2 x_{0}^{2}}}$

'prob_id: 4, err: 3.3746957690291797e-06'

$\displaystyle \displaystyle \frac{x_{0} \left(c_{2} - c_{4} x_{0}\right) + \left(c_{1} + c_{3} x_{0}\right) e^{e^{- 2 x_{0}^{2}}}}{x_{0}}$

'prob_id: 4, err: 3.3811044286786395e-06'

$\displaystyle \displaystyle c_{1} e^{x_{0}^{2}} + \frac{c_{2}}{x_{0}} + c_{3} - c_{3} e^{- 2 x_{0}^{2}} - c_{4} e^{- x_{0}^{2}}$

'prob_id: 4, err: 3.3842683416733736e-06'

$\displaystyle \displaystyle \frac{- c_{4} + x_{0} \left(- c_{2} + c_{3} x_{0}\right) + \left(c_{1} x_{0} + c_{4}\right) e^{x_{0} - e^{2 x_{0}}}}{x_{0}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  5

'prob_id: 5, err: 1.686027444316002e-05'

$\displaystyle \displaystyle c_{1} x_{0} + c_{1} e^{- x_{0}^{4}} + \frac{c_{1}}{x_{0}^{2}} + c_{2} - 2 c_{3} - \frac{c_{3}}{x_{0}^{3}} - 2 c_{4} x_{0} - \frac{c_{4}}{x_{0}^{2}}$

'prob_id: 5, err: 1.686067254813111e-05'

$\displaystyle \displaystyle \frac{x_{0}^{3} \left(- c_{2} + c_{4} e^{x_{0}}\right) + \left(- c_{1} x_{0} + c_{3}\right) e^{x_{0}}}{x_{0}^{3}}$

'prob_id: 5, err: 1.686069307097475e-05'

$\displaystyle \displaystyle \frac{c_{2} x_{0}^{2} + c_{4} + x_{0}^{2} - x_{0} \left(c_{1} + c_{3} x_{0}\right) \left(c_{4} + x_{0}^{2}\right)}{x_{0} \left(c_{4} + x_{0}^{2}\right)}$

'prob_id: 5, err: 1.6860856181522074e-05'

$\displaystyle \displaystyle \frac{c_{1}}{x_{0}^{3}} + c_{2} x_{0} - c_{3} - \frac{c_{4}}{x_{0}}$

'prob_id: 5, err: 1.686098183474468e-05'

$\displaystyle \displaystyle c_{1} e^{x_{0}} + c_{2} + \frac{c_{3}}{x_{0}^{2}} - \frac{c_{4}}{x_{0}^{3}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  6

'prob_id: 6, err: 9.922429392571683e-06'

$\displaystyle \displaystyle - c_{2} - c_{3} e^{- x_{0}^{2}} + \frac{2 c_{4}}{c_{1} + x_{0}} - e^{- \left(c_{1} + x_{0}\right)^{2}} + e^{- c_{4}^{2}}$

'prob_id: 6, err: 9.936575700754542e-06'

$\displaystyle \displaystyle \frac{c_{2} + x_{0}^{2} \left(c_{1} x_{0} \left(c_{4} + x_{0}\right) + c_{3}\right) - x_{0} \left(c_{1} x_{0} \left(c_{4} + x_{0}\right) + c_{4}\right)}{x_{0}^{2}}$

'prob_id: 6, err: 9.936942645025763e-06'

$\displaystyle \displaystyle c_{1} e^{- e^{- 2 x_{0}^{2}}} + \frac{c_{2} e^{- x_{0}^{2}}}{x_{0}} + c_{3} + c_{4} - \frac{c_{4}}{x_{0}}$

'prob_id: 6, err: 9.937353947520078e-06'

$\displaystyle \displaystyle - c_{1} + c_{2} e^{x_{0}} - \frac{c_{3}}{x_{0}} + \frac{c_{4} e^{- e^{2 x_{0}}}}{c_{2} + e^{x_{0}}}$

'prob_id: 6, err: 9.938981126078224e-06'

$\displaystyle \displaystyle c_{1} + c_{2} e^{- x_{0}} - \frac{c_{3} e^{- x_{0}^{2} - x_{0}}}{x_{0}} + \frac{c_{4} e^{- x_{0}}}{x_{0}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  7

'prob_id: 7, err: 8.515167695863056e-06'

$\displaystyle \displaystyle - c_{1} e^{e^{- x_{0}^{2}}} + c_{2} + c_{3} x_{0} - c_{4} e^{- x_{0}^{2}} + x_{0} e^{- x_{0}^{2}}$

'prob_id: 7, err: 8.519576231706857e-06'

$\displaystyle \displaystyle - c_{1} e^{x_{0}} + c_{1} e^{- e^{2 x_{0}}} - c_{2} + c_{3} e^{x_{0} - e^{2 x_{0}}} - c_{3} e^{- 2 e^{2 x_{0}}} + c_{4} e^{e^{x_{0}}}$

'prob_id: 7, err: 8.522266408037304e-06'

$\displaystyle \displaystyle c_{1} e^{- x_{0}^{2}} + c_{2} - c_{3} x_{0} - c_{4} x_{0} e^{- x_{0}^{2}} + e^{e^{- x_{0}^{2}}}$

'prob_id: 7, err: 8.569811491073491e-06'

$\displaystyle \displaystyle - c_{1} x_{0} + c_{2} e^{x_{0}} + c_{3} + c_{4} e^{- e^{2 x_{0}}} + e^{- e^{- 2 e^{2 x_{0}}}} - e^{- e^{2 x_{0}}}$

'prob_id: 7, err: 8.596454393800356e-06'

$\displaystyle \displaystyle \left(- c_{1} + c_{2} x_{0} + \left(- c_{3} + c_{4} e^{x_{0}^{2}} + x_{0}\right) e^{x_{0}^{2}}\right) e^{- x_{0}^{2}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  8

'prob_id: 8, err: 5.7033656245193685e-06'

$\displaystyle \displaystyle \frac{\left(x_{0} \left(c_{1} x_{0} - c_{3} + e^{c_{2}}\right) e^{c_{1} x_{0} \left(c_{3} - e^{c_{2}}\right)} + \left(- c_{2} x_{0} + c_{4}\right) e^{x_{0}^{2}}\right) e^{- x_{0} \left(c_{1} \left(c_{3} - e^{c_{2}}\right) + x_{0}\right)}}{x_{0}}$

'prob_id: 8, err: 5.703378409998452e-06'

$\displaystyle \displaystyle c_{1} e^{- x_{0}^{2}} + c_{2} + c_{3} x_{0} e^{- x_{0}^{2}} + \frac{c_{4}}{x_{0}} + x_{0} e^{- x_{0}^{2}}$

'prob_id: 8, err: 5.7033784099984615e-06'

$\displaystyle \displaystyle c_{1} e^{- x_{0}^{2}} + \frac{c_{2}}{x_{0}} - c_{3} - c_{4} x_{0} e^{- x_{0}^{2}}$

'prob_id: 8, err: 5.705047245789752e-06'

$\displaystyle \displaystyle c_{1} - c_{2} c_{3} - c_{2} c_{4} e^{- x_{0}^{2}} + c_{2} + \frac{c_{2}}{x_{0}} - c_{3} x_{0} - c_{4} x_{0} e^{- x_{0}^{2}} + x_{0} + 1$

'prob_id: 8, err: 5.705078353147797e-06'

$\displaystyle \displaystyle - c_{1} x_{0} + \frac{c_{2}}{x_{0}} - c_{3} + c_{4} x_{0} e^{- x_{0}^{2}} - x_{0}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  9

'prob_id: 9, err: 4.523905989067585e-06'

$\displaystyle \displaystyle 2 c_{1} + \frac{c_{1}}{x_{0}^{2}} + c_{2} - c_{3} x_{0} + \frac{4 c_{4}}{x_{0}} + \frac{c_{4}}{x_{0}^{3}}$

'prob_id: 9, err: 4.523956586681867e-06'

$\displaystyle \displaystyle - c_{1} x_{0} - c_{2} - c_{3} - \frac{c_{3}}{x_{0}^{2}} + \frac{3 c_{4}}{x_{0}} + \frac{c_{4}}{x_{0}^{3}}$

'prob_id: 9, err: 4.524279590137839e-06'

$\displaystyle \displaystyle \frac{c_{2} - c_{4} x_{0} + x_{0}^{3} \left(c_{1} + c_{3} c_{4} x_{0}\right) + x_{0}}{x_{0}^{3}}$

'prob_id: 9, err: 4.524279590138164e-06'

$\displaystyle \displaystyle \frac{- c_{4} + x_{0}^{3} \left(- c_{1} x_{0} + c_{2}\right) + x_{0} \left(c_{1} + c_{3}\right)}{x_{0}^{3}}$

'prob_id: 9, err: 4.651129097622205e-06'

$\displaystyle \displaystyle c_{1} x_{0} + \frac{c_{2}}{x_{0}} + \frac{c_{3}}{x_{0}^{2}} + \frac{c_{4} e^{- x_{0}}}{x_{0}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  10

'prob_id: 10, err: 1.9017543270061446e-05'

$\displaystyle \displaystyle \frac{c_{2} e^{\frac{1}{x_{0}}} - c_{3} + x_{0} \left(- c_{1} x_{0} + c_{4}\right)}{x_{0}}$

'prob_id: 10, err: 1.9104544589813626e-05'

$\displaystyle \displaystyle - \frac{c_{1}}{\frac{c_{4}}{x_{0}^{3}} - x_{0}} + c_{3} + \frac{c_{4} e^{\frac{1}{x_{0}}}}{x_{0}^{3}}$

'prob_id: 10, err: 1.9158737383062652e-05'

$\displaystyle \displaystyle c_{1} x_{0}^{2} + c_{2} + \frac{c_{3}^{2}}{x_{0}^{6}} - \frac{c_{3}}{x_{0}} + \frac{c_{3}}{x_{0}^{5}} - \frac{c_{3}}{x_{0}^{6}} + c_{4} x_{0}$

'prob_id: 10, err: 1.9240171327253178e-05'

$\displaystyle \displaystyle - 2 c_{1} + \frac{c_{2}}{x_{0}^{3}} - \frac{c_{3}}{x_{0}^{4}} - \frac{c_{4}}{x_{0}}$

'prob_id: 10, err: 1.9291883990542647e-05'

$\displaystyle \displaystyle - c_{1} x_{0} + c_{2} e^{x_{0}^{2}} - c_{3} + \frac{c_{4}}{x_{0}^{4}}$

---------------------------------------------------------
---------------------------------------------------------
Best five fits for id:  11

'prob_id: 11, err: 1.1337997121125522e-05'

$\displaystyle \displaystyle \frac{c_{2} \left(c_{4} - x_{0}^{4}\right) - c_{3} x_{0} \left(c_{4} - x_{0}^{4}\right) + x_{0} \left(- c_{1} x_{0}^{2} - c_{2} x_{0} + c_{4}\right)}{x_{0} \left(c_{4} - x_{0}^{4}\right)}$

'prob_id: 11, err: 1.135016956476325e-05'

$\displaystyle \displaystyle - c_{1} - \frac{c_{3}}{x_{0} - e^{c_{3}}} + \frac{c_{2} + \frac{c_{4}}{x_{0}} + e^{c_{4}}}{x_{0}}$

'prob_id: 11, err: 1.1360665073366816e-05'

$\displaystyle \displaystyle - c_{1} + \frac{c_{1}}{x_{0}^{4}} + c_{2} - \frac{c_{3}}{x_{0}^{2}} - c_{4} x_{0} + \frac{c_{4}}{x_{0}^{3}}$

'prob_id: 11, err: 1.1364062900679142e-05'

$\displaystyle \displaystyle - c_{1} x_{0} + c_{2} x_{0}^{2} - c_{2} x_{0} e^{- e^{- 2 x_{0}^{2}}} + c_{3} e^{e^{- 2 x_{0}^{2}}} + c_{4}$

'prob_id: 11, err: 1.138267448015574e-05'

$\displaystyle \displaystyle \left(- c_{2} e^{x_{0}^{2} + e^{- 2 x_{0}^{2}}} + \left(c_{1} + \left(c_{3} - c_{4} x_{0}\right) e^{x_{0}^{2}}\right) e^{x_{0}^{2}} - 1\right) e^{- x_{0}^{2} - e^{- 2 x_{0}^{2}}}$

---------------------------------------------------------