Differentiable Cartesian Genetic Programming (dCGP)

Differentiable Cartesian Genetic Programming (dCGP) is a recent development of CGP that adds the information about the derivatives of the output nodes (the programs, or expressions encoded) with respect to the input nodes (the input values) and/or the weights (that can be associated with every connection in the graph, similarly to Neural Networks).

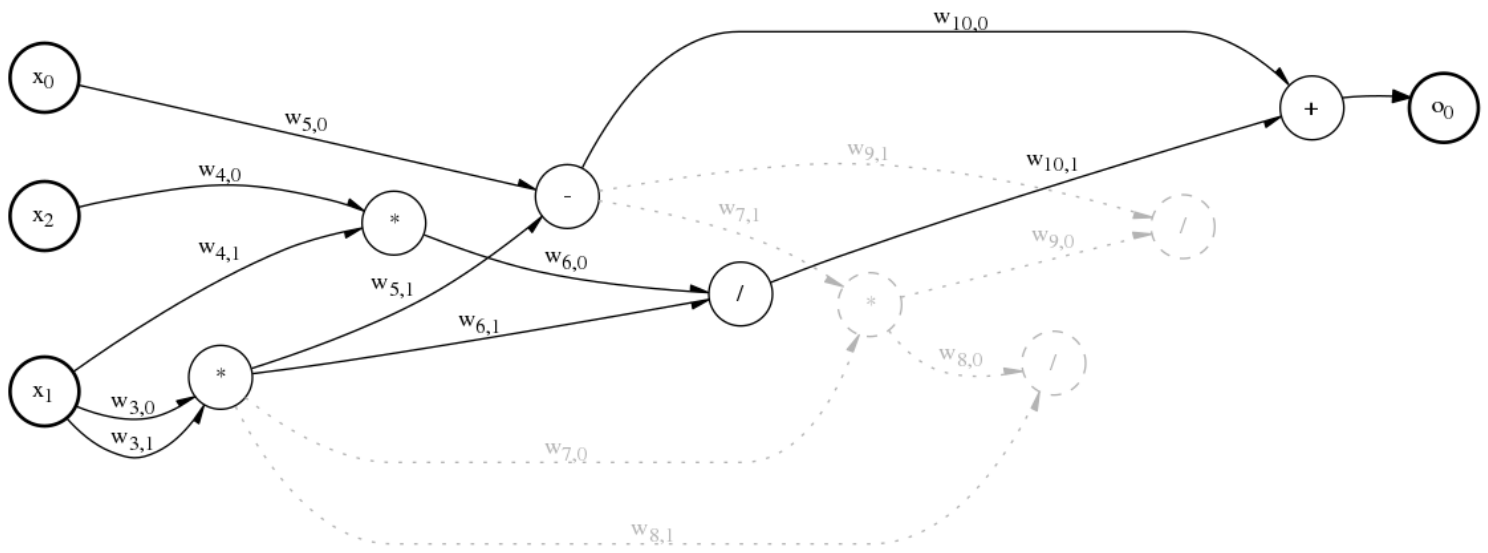
A weighted dCGP expression

The derivatives are obtained by means of Automatic Differentiation through the AuDi library, that implements the Taylor truncated polynomial algebra.

The use of the derivatives of the outputs (and hence of any fitness function that is a combination of these) with respect to inputs/weights enables a number of new applications currently the subject of active research.

The evolution of the genetic program can now be supported by using the information on the derivatives, hence enabling for the equivalent of back-propagation in Neural Networks.

Furthermore, the fitness function itself can be defined in terms of the derivatives, allowing dCGP to encode solutions to initial value problems, boundary value problems, Lyapunov functions, etc.

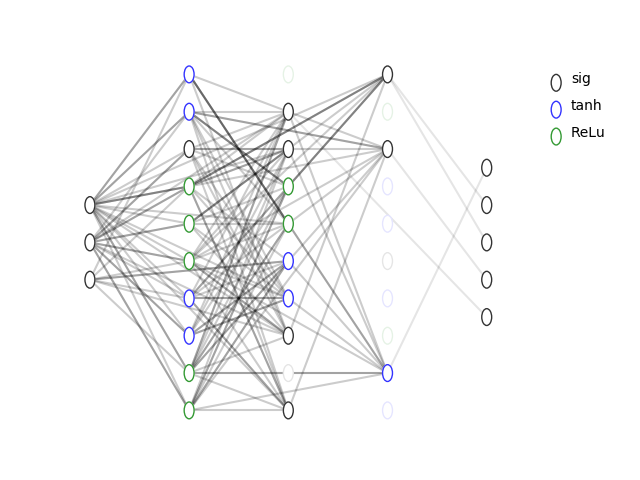
A dCGP-ANN expression

Possible applications of a dCGP are:

• Symbolic Regression.

• Solving differential equations.

• Searching for Lyapunov functions (in non-linear control problems).

• Searching for conserved quantities in dynamical systems.

• Concurrent learning of network topologies and parameters.

In [dCGP1] we introduce the ideas behind dCGP and study a few interesting applications. we present an extension to the normal, canonical CGP, which introduces weights on the node connections and allows for a variable number of model parameters, albeit complicating the learning process.

In [dCGP2] we introduce a further new variant of a canonical CGP, the dCGP-ANN, which makes use of backpropagation to learn the many model parameters (biases and weights) of an artificial neural network represented by the CGP encoding.